ENERGIA

El concepto de energíaestá relacionado con la capacidad de generar movimientoo lograr la transformación de algo. En el ámbito económico y tecnológico, la energía hace referencia a un recurso natural y los elementos asociados que permiten hacer un uso industrial del mismo.

Por ejemplo: “El país tiene serios problemas de energía por la falta de inversiones”, “Gómez es un jugador de mucha energía, capaz de cambiarle la fisonomía al equipo”, “En la última semana, ya se ha cortado la energía tres veces”.

http://definicion.de/energia/

FUERZA

Descomposición de las fuerzas que actúan sobre un sólido situado en un plano inclinado.

En física, la fuerza es una magnitud vectorial que mide la razón de cambio de momento lineal entre dos partículas o sistemas de partículas. Según una definición clásica, fuerza es todo agente capaz de modificar la cantidad de movimiento o la forma de los materiales. No debe confundirse con los conceptos de esfuerzo o de energía.

En el Sistema Internacional de Unidades, la unidad de medida de fuerza es el newton que se representa con el símbolo: N , nombrada así en reconocimiento a Isaac Newton por su aportación a la física, especialmente a la mecánica clásica. El newton es una unidad derivada del SI que se define como la fuerza necesaria para proporcionar una aceleraciónde 1 m/s² a un objeto de 1 kg de masa.

MOVIMIENTO ARMONICO SIMPLE

El movimiento armónico simple (m.a.s.), también denominado movimiento vibratorio armónico simple (m.v.a.s.), es un movimiento periódico, y vibratorio en ausencia de fricción, producido por la acción de una fuerza recuperadora que es directamente proporcional a la posición, y que queda descrito en función del tiempo por una función senoidal (seno o coseno). Si la descripción de un movimiento requiriese más de una función armónica, en general sería un movimiento armónico, pero no un m.a.s.

En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s. oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función del tiempo con respecto a ese punto es una sinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste.

NORMALIDAD

La normalidad (N) es el número de equivalentes (eq-g) de soluto (sto) entre el volumen de la disolución en litros (L)

${\displaystyle N={\frac {eqg_{sto}}{V_{L}}}}$

Normalidad ácido-base Es la normalidad de una disolución cuando se utiliza para una reacción como ácido o como base. Por esto suelen titularse utilizando indicadores de pH.^[8]

En este caso, los equivalentes pueden expresarse de la siguiente forma:

${\displaystyle n={moles}\cdot {H^{+}}}$ para un ácido, o ${\displaystyle n={moles}\cdot {OH^{-}}}$ para una base.

Donde:

• moles es la cantidad de moles.
• OH^– es la cantidad de hidroxilos cedidos por una molécula de la base.

Por esto, podemos decir lo siguiente:

${\displaystyle N={M}\cdot {H^{+}}}$ para un ácido, o ${\displaystyle N={M}\cdot {OH^{-}}}$ para una base.

Donde:

• M es la molaridad de la disolución.
• H⁺ es la cantidad de protones cedidos por una molécula del ácido.
• OH^– es la cantidad de hidroxilos cedidos por una molécula de la base.

Ejemplos:

• Una disolución 1 M de HCl cede 1 H⁺, por lo tanto, es una disolución 1 N.
• Una disolución 1 M de Ca (OH)₂ cede 2 OH^–, por lo tanto, es una disolución 2 N.

MOLALIDAD

La molalidad (m) es el número de moles de soluto que contiene un kilogramo de solvente. Para preparar disoluciones de una determinada molalidad, no se emplea un matraz aforado como en el caso de la molaridad, sino que se puede hacer en un vaso de precipitados y pesando con una balanza analítica, previo peso del vaso vacío para poderle restar el correspondiente valor.

${\displaystyle m={\frac {\mbox{moles de soluto (n)}}{\mbox{masa de disolvente (kg)}}}}$

La principal ventaja de este método de medida respecto a la molaridad es que como el volumen de una disolución depende de la temperatura y de la presión, cuando éstas cambian, el volumen cambia con ellas. Gracias a que la molalidad no está en función del volumen, es independiente de la temperatura y la presión, y puede medirse con mayor precisión.

Es menos empleada que la molaridad pero igual de importante.

MOLARIDAD

La molaridad (M), o concentración molar, es la cantidad de sustancia (n) de soluto por cada litro de disolución. Por ejemplo, si se disuelven 0, 5 moles de soluto en 1000 mL de disolución, se tiene una concentración de ese soluto de 0,5  M (0, 5 molar). Para preparar una disolución de esta concentración habitualmente se disuelve primero el soluto en un volumen menor, por ejemplo 300 mL, y se traslada esa disolución a un matraz aforado, para después enrasarlo con más disolvente hasta los 1000 mL.

Es el método más común de expresar la concentración en química, sobre todo cuando se trabaja con reacciones químicas y relaciones estequiométricas. Sin embargo, este proceso tiene el inconveniente de que el volumen cambia con la temperatura.

Se representa también como: M = n / V, en donde "n" es la cantidad de sustancia (n= mol soluto/masa molar) y "V" es el volumen de la disolución expresado en litros.

PORCENTAJE VOLUMEN VOLUMEN

orcentaje volumen-volumen (%v/v)Editar

Expresa el volumen de soluto por cada cien unidades de volumen de la disolución. Se suele usar para mezclas líquidas o gaseosas, en las que el volumen es un parámetro importante a tener en cuenta. Es decir, el porcentaje que representa el soluto en el volumen total de la disolución. Suele expresarse simplificadamente como «% v/v».

${\displaystyle \ \%{\mbox{ volumen}}={\frac {\mbox{volumen de soluto (ml)}}{{\mbox{volumen de disolución (ml}})}}\cdot 100}$

Por ejemplo, si se tiene una disolución del 20% en volumen (20 % v/v) de alcohol en agua quiere decir que hay 20 ml de alcohol por cada 100 ml de disolución.

La graduación alcohólica de las bebidas se expresa precisamente así: un vino de 12 grados (12°) tiene un 12% (v/v) de alcohol.

PORCENTAJE MASA MASA

Porcentaje masa-masa (%  m/m)Editar

Se define como la masa de soluto (sustancia que se disuelve) por cada 100 unidades de masa de la solución:

${\displaystyle \%{\mbox{ masa}}={\frac {\mbox{masa de soluto (g)}}{\mbox{masa de disolución (g)}}}\cdot 100}$

Por ejemplo, si se disuelven 20 g de azúcar en 80 g de agua, el porcentaje en masa será: [20/(80+20)]x 100=20% o, para distinguirlo de otros porcentajes, 20% m/m (en inglés, %w/w)

ENERGIA

Energía

Para otros usos de este término, véase Energía (desambiguación).

Un rayo es una forma de transmisión de energía.

El término energía (del griego ἐνέργεια enérgeia, «actividad», «operación»; de ἐνεργóς energós, «fuerza de acción» o «fuerza de trabajo») tiene diversas acepciones y definiciones, relacionadas con la idea de una capacidad para obrar, surgir, transformar o poner en movimiento.

En física, «energía» se define como la capacidad para realizar un trabajo. En tecnología y economía, «energía» se refiere a un recurso natural (incluyendo a su tecnología asociada) para poder extraerla, transformarla y darle un uso industrial o económico.

FUERZA

En https://www.youtube.com/watch?v=Vr7F1ENbpeMfísica, la fuerza es una magnitud vectorial que mide la razón de cambio de momento lineal entre dos partículas o sistemas de partículas. Según una definición clásica, fuerza es todo agente capaz de modificar la cantidad de movimiento o la forma de los materiales. No debe confundirse con los conceptos de esfuerzo o de energía.

En el Sistema Internacional de Unidades, la unidad de medida de fuerza es el newton que se representa con el símbolo: N , nombrada así en reconocimiento a Isaac Newton por su aportación a la física, especialmente a la mecánica clásica. El newton es una unidad derivada del SI que se define como la fuerza necesaria para proporcionar una aceleración de 1 m/s² a un objeto de 1 kg de masa.

Fuerza gravitatoria[editar]

Fuerzas gravitatorias entre dos partículas.

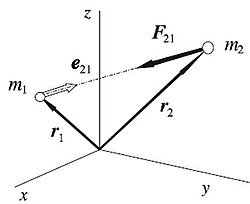
En mecánica newtoniana la fuerza de atracción entre dos masas, cuyos centros de gravedad están lejos comparadas con las dimensiones del cuerpo,² viene dada por la ley de la gravitación universal de Newton:

${\displaystyle \mathbf {F} _{21}=-G{\frac {m_{1}m_{2}}{|\mathbf {r} _{21}|^{2}}}\mathbf {e} _{21}=-G{\frac {m_{1}m_{2}}{|\mathbf {r} _{21}|^{3}}}\mathbf {r} _{21}}$

Donde:

${\displaystyle \mathbf {F} _{21}}$ es la fuerza que actúa sobre el cuerpo 2, ejercida por el cuerpo 1.

${\displaystyle G\,}$ constante de la gravitación universal.

${\displaystyle \mathbf {r} _{21}=\mathbf {r} _{2}-\mathbf {r} _{1}}$ vector de posición relativo del cuerpo 2 respecto al cuerpo 1.

${\displaystyle \mathbf {e} _{21}}$ es el vector unitario dirigido desde 1 hacía 2.

${\displaystyle m_{1},m_{2}\,}$ masas de los cuerpos 1 y 2.

Cuando la masa de uno de los cuerpos es muy grande en comparación con la del otro (por ejemplo, si tiene dimensiones planetarias), la expresión anterior se transforma en otra más simple:

${\displaystyle \mathbf {F} =-m\left(G{\frac {M}{R_{0}^{2}}}\right){\hat {\mathbf {u} }}_{r}=-mg{\hat {\mathbf {u} }}_{r}=m\mathbf {g} }$

Donde:

${\displaystyle \mathbf {F} }$ es la fuerza del cuerpo de gran masa ("planeta") sobre el cuerpo pequeño.

${\displaystyle \mathbf {u} _{r}}$ es un vector unitario dirigido desde el centro del "planeta" al cuerpo de pequeña masa.

${\displaystyle R_{0}\,}$ es la distancia entre el centro del "planeta" y el del cuerpo pequeño.

Véase también: Gravedad

Fuerzas de campos estacionarios[editar]

Artículo principal: Campo (física)

En mecánica newtoniana también es posible modelizar algunas fuerzas constantes en el tiempo como campos de fuerza. Por ejemplo la fuerza entre dos cargas eléctricas inmóviles, puede representarse adecuadamente mediante la ley de Coulomb:

${\displaystyle \mathbf {F} _{12}=-\kappa {\frac {q_{1}q_{2}}{\|\mathbf {r} _{12}\|^{3}}}\mathbf {r} _{12}}$

Donde:

${\displaystyle \mathbf {F} _{12}}$ es la fuerza ejercida por la carga 1 sobre la carga 2.

${\displaystyle \kappa \,}$ una constante que dependerá del sistema de unidades para la carga.

${\displaystyle \mathbf {r} _{12}}$ vector de posición de la carga 2 respecto a la carga 1.

${\displaystyle q_{1},q_{2}\,}$ valor de las cargas.

También los campos magnéticos estáticos y los debidos a cargas estáticas con distribuciones más complejas pueden resumirse en dos funciones vectoriales llamadas campo eléctrico y campo magnético tales que una partícula en movimiento respecto a las fuentes estáticas de dichos campos viene dada por la expresión de Lorentz:

${\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}$

Donde:

${\displaystyle \mathbf {E} }$ es el campo eléctrico.

${\displaystyle \mathbf {B} }$ es el campo magnético.

${\displaystyle \mathbf {v} }$ es la velocidad de la partícula.

${\displaystyle q\,}$ es la carga total de la partícula.

Los campos de fuerzas no constantes sin embargo presentan una dificultad especialmente cuando están creados por partículas en movimiento rápido, porque en esos casos los efectos relativistas de retardo pueden ser importantes, y la mecánica clásica, da lugar a un tratamiento de acción a distancia que puede resultar inadecuado si las fuerzas cambian rápidamente con el tiempo.

Fuerza eléctrica[editar]

La fuerza eléctrica también son de acción a distancia, pero a veces la interacción entre los cuerpos actúa como una fuerza atractiva mientras que, otras veces, tiene el efecto inverso, es decir puede actuar como una fuerza repulsiva.

Unidades de fuerza[editar]

En el Sistema Internacional de Unidades (SI) y en el Cegesimal (cgs), el hecho de definir la fuerza a partir de la masa y la aceleración (magnitud en la que intervienen longitud y tiempo), conlleva a que la fuerza sea una magnitud derivada. Por el contrario, en el Sistema Técnico la fuerza es una Unidad Fundamental y a partir de ella se define la unidad de masa en este sistema, la unidad técnica de masa, abreviada u.t.m. (no tiene símbolo). Este hecho atiende a las evidencias que posee la física actual, expresado en el concepto de fuerzas fundamentales, y se ve reflejado en el Sistema Internacional de Unidades.

• Sistema Internacional de Unidades (SI)
  • newton (N)
• Sistema Técnico de Unidades
  • kilogramo-fuerza (kg_f) o kilopondio (kp)
• Sistema Cegesimal de Unidades
  • dina (dyn)
• Sistema anglosajón de unidades
  • Poundal
  • Libra fuerza (lb_f)
  • KIP (= 1000 lb_f)

Equivalencias

1 newton = 100 000 dinas

1 kilogramo-fuerza = 9.806 65 newtons

1 libra fuerza ≡ 4.448 222 newtons

Fuerza en mecánica relativista[editar]

En relatividad especial la fuerza se debe definir solo como derivada del momento lineal, ya que en este caso la fuerza no resulta simplemente proporcional a la aceleración:

${\displaystyle \mathbf {F} ={\frac {d}{dt}}\left({\frac {m\mathbf {v} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\right)={\frac {m\mathbf {v} }{\left[1-{\frac {v^{2}}{c^{2}}}\right]^{3/2}}}\left({\frac {\mathbf {v} }{c^{2}}}\cdot \mathbf {a} \right)+{\frac {m\mathbf {a} }{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

De hecho en general el vector de aceleración y el de fuerza ni siquiera serán paralelos, solo en el movimiento circular uniforme y en cualquier movimiento rectilíneo serán paralelos el vector de fuerza y aceleración pero en general se el módulo de la fuerza dependerá tanto de la velocidad como de la aceleración.

"Fuerza" gravitatoria[editar]

En la teoría de la relatividad general el campo gravitatorio no se trata como un campo de fuerzas real, sino como un efecto de la curvatura del espacio-tiempo. Una partícula másica que no sufre el efecto de ninguna otra interacción que la gravitatoria seguirá una trayectoria geodésica de mínima curvatura a través del espacio-tiempo, y por tanto su ecuación de movimiento será:

${\displaystyle {\cfrac {d^{2}x^{\mu }}{ds^{2}}}+\sum _{\sigma ,\nu }\Gamma _{\sigma \nu }^{\mu }{\cfrac {dx^{\sigma }}{ds}}{\cfrac {dx^{\nu }}{ds}}=0}$

Donde:

${\displaystyle x^{\mu }\,}$ son las coordenadas de posición de la partícula.

${\displaystyle s\,}$ el parámetro de arco, que es proporcional al tiempo propio de la partícula.

${\displaystyle \Gamma _{\sigma \nu }^{\mu }\,}$ son los símbolos de Christoffel correspondientes a la métrica del espacio-tiempo.

La fuerza gravitatoria aparente procede del término asociado a los símbolos de Christoffel. Un observador en "caída libre" formará un sistema de referencia en movimiento en el que dichos símbolos de Christoffel son nulos, y por tanto no percibirá ninguna fuerza gravitatoria tal como sostiene el principio de equivalencia que ayudó a Einstein a formular sus ideas sobre el campo gravitatorio.

Fuerza electromagnética[editar]

El efecto del campo electromagnético sobre una partícula relativista viene dado por la expresión covariante de la fuerza de Lorentz:

${\displaystyle f_{\alpha }=\sum _{\beta }q\ F_{\alpha \beta }\ u^{\beta }\,}$

Donde:

${\displaystyle f_{\alpha }\,}$ son las componentes covariantes de la cuadrifuerza experimentada por la partícula.

${\displaystyle F_{\alpha \beta }\,}$ son las componentes del tensor de campo electromagnético.

${\displaystyle u^{\alpha }\,}$ son las componentes de la cuadrivelocidad de la partícula.

La ecuación de movimiento de una partícula en un espacio-tiempo curvo y sometida a la acción de la fuerza anterior viene dada por:

${\displaystyle m{\frac {Du^{\mu }}{D\tau }}=m\left({\cfrac {d^{2}x^{\mu }}{d\tau ^{2}}}+\Gamma _{\sigma \nu }^{\mu }{\cfrac {dx^{\sigma }}{d\tau }}{\cfrac {dx^{\nu }}{d\tau }}\right)=f^{\mu }}$

Donde la expresión anterior se ha aplicado el convenio de sumación de Einstein para índices repetidos, el miembro de la derecha representa la cuadriaceleración y siendo las otras magnitudes:

${\displaystyle f^{\mu }=g^{\mu \alpha }f_{\alpha }\,}$ son las componentes contravarianetes de la cuadrifuerza electromagnética sobre la partícula.

${\displaystyle m\,}$ es la masa de la partícula.